DDA 是数字微分分析式(digital differential analyzer)的缩写。DDA算法是一种基于直线的微分方程来生成直线的方法。
算法思想
设直线的起点为(x1, y1),终点为(x2, y2),则直线的斜率为:
$$ m = \frac{y2-y1}{x2-x1} = \frac{dy}{dx} $$
直线中每一点坐标都可由前一点坐标变化一个增量得到,即表现为递归式:
$$ x_{i+1} = x_i + Dx $$
$$ y_{i+1} = y_i + Dy $$
又有 $Dy = m * Dx$
递归式初值为起点 $(x_1, y_1)$,这样就可以用加法来生成一条直线。
具体步骤为:
按直线起点到终点的方向不同,将直角坐标系分成8个象限。
分析发现,当 $ |dx| > |dy| $ 时,$ |Dx| = 1, |Dy| = m $;否则,$ |Dx| = \frac{1}{m}, |Dy| = 1 $。
Dx, Dy 的符号与 dx, dy 的符号相同。
算法实现
1 | function dda_line(ctx, xa, ya, xb, yb) { |
用canvas模拟算法实现效果图
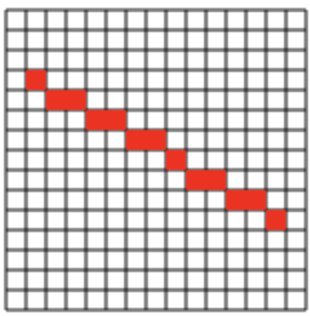
算法优缺点
优点:
- 易理解
- 速度快
缺点:
- 涉及到小数计算,对硬件不友好