本算法是bresenham在1965年提出的。它是从计算机硬件的角度和图像的光栅化过程来生成直线的。
算法思想
设直线的起点为(x1, y1),终点为(x2, y2),则直线可以表示为:$ y = m * x + b $
先假设直线在第一象限,每次光栅化时:$ x_{i+1} = x_i + 1 $
根据图像光栅化过程:$ y_{i+1} = y_i $,
或者 $ y_{i+1} = y_i+1 $
而根据直线方程:$ y = m * (x_i + 1) + b $
这样就能得到理论值与光栅后的值的误差:
$$ d1 = y - y_i $$
$$ d2 = (y_i + 1) - y $$
如果 $ d1 - d2 > 0 $,则 $ y_{i+1} = y_i + 1 $ ,
否则 $ y_{i+1} = y_i $
因此算法的关键在于确定 $ d1 - d2 $ 的符号。
算法实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| function bresenham_line(ctx, x1, y1, x2, y2) {
var dx, dy, x, y, p, const1, const2, inc, tmp;
dx = x2 - x1;
dy = y2 - y1;
if (dx * dy >= 0) {
inc = 1;
} else {
inc = -1;
}
if (Math.abs(dx) > Math.abs(dy)) {
if (dx < 0) {
tmp = x1;
x1 = x2;
x2 = tmp;
tmp = y1;
y1 = y2;
y2 = tmp;
dx = -dx;
dy = -dy;
}
p = 2 * dy - dx;
const1 = 2 * dy;
const2 = 2 * (dy - dx);
x = x1;
y = y1;
selectGrid(ctx, x, y);
while (x < x2) {
x++;
if (p < 0) {
p += const1;
} else {
y += inc;
p += const2;
}
selectGrid(ctx, x, y);
}
} else {
if (dy < 0) {
tmp = x1;
x1 = x2;
x2 = tmp;
tmp = y1;
y1 = y2;
y2 = tmp;
dx = -dx;
dy = -dy;
}
p = 2 * dx - dy;
const1 = 2 * dx;
const2 = 2 * (dx - dy);
x = x1;
y = y1;
selectGrid(ctx, x, y);
while (y < y2) {
y++;
if (p < 0) {
p += const1;
} else {
x += inc;
p += const2;
}
selectGrid(ctx, x, y);
}
}
}
|
用canvas模拟算法实现效果图
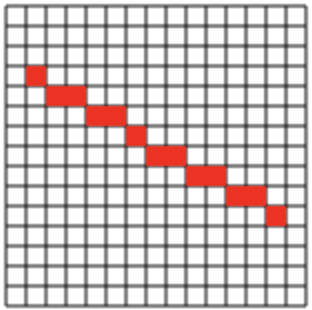
算法优缺点
优点:
- 不必计算直线的斜率,因此不做除法
- 不用浮点数,只用整数
- 速度快,适用于硬件实现
